Operasi Pecahan
Pengertian Pecahan
Pecahan adalah bilangan rasional yang ditulis dalam bentuk a/b. Dengan ketentuan, a merupakan pembilang dan b merupakan penyebut. Sebagai penyebut, syarat yang harus dipenuhi b adalah b ≠ 0. Artinya, nilai b tidak boleh sama dengan nol. Agar lebih mudah umtk dipahami mulanya kue tart utuh, lalu dipotong menjadi empat bagian sama besar. Nah, setiap bagian potongan itu bisa dinyatakan sebagai 1 dari total empat potongan atau satu per empat. Secara matematis, bisa ditulis sebagai 1/4 bagian.
Macam-Macam Pecahan
Adapun macam-macam pecahan yang harus Quipperian ketahui adalah sebagai berikut.
1. Pecahan sejati atau pecahan murni
Pecahan sejati atau murni merupakan bentuk yang paling sederhana. Artinya, bilangan ini tidak bisa disederhanakan lagi menjadi bilangan yang lebih kecil.
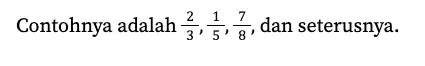
2. Pecahan campuran
Disebut campuran karena terdiri dari bilangan pecah dan utuh.

3. Pecahan desimal
Disebut desimal karena penyebutnya berupa bilangan 10, 100, 1.000, dan seterusnya.

4. Pecahan senilai
Disebut senilai karena memiliki nilai akhir atau hasil pembagian yang sama.

5. Pecahan senama
Disebut senama karena memiliki penyebut yang sama.
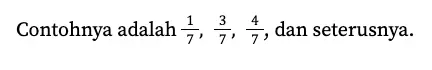
Operasi Bilangan Pecahan
Setelah membahas pengertian dan macamnya, kali ini Quipper Blog mau mengenalkan operasi bilangan pecahan.
Bentuk operasinya sama seperti operasi bilangan lain, yaitu memuat penjumlahan, pengurangan, perkalian, dan pembagian.
Untuk lebih jelasnya, check this out!
1. Penjumlahan pecahan
Secara umum, penjumlahan pecahan dibagi menjadi dua, yaitu penjumlahan dengan penyebut sama dan penjumlahan dengan penyebut berbeda.
a. Penjumlahan pecahan berpenyebut sama
Untuk bilangan yang penyebutnya sama caranya cukup mudah, yaitu dengan menjumlahkan pembilangnya saja. Berikut ini contohnya.
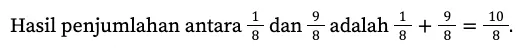
b. Penjumlahan pecahan berpenyebut berbeda
Hasil penjumlahan antara bilangan berpenyebut berbeda tentu lebih rumit daripada berpenyebut sama, yaitu dengan menyamakan penyebutnya terlebih dahulu. Berikut ini contohnya.

Pertama, tentukan dahulu bilangan yang bisa mewakili kedua penyebut (3 dan 5). Apakah 6 bisa mewakili keduanya?
Tentu tidak karena hasil pembagian antara 6 dan 5 menghasilkan bilangan tidak bulat.
Apakah 15 bisa mewakili keduanya? Iya, karena hasil bagian antara 15 dan 5 serta 15 dan 3 akan menghasilkan bilangan bulat.
Dengan kata lain, Quipperian bisa mencari nilai KPK antara 3 dan 5 agar diperoleh nilai penyebut yang sama.
Jika sudah mendapatkan KPKnya, silakan lakukan langkah berikut.
Bagi KPK dengan masing-masing penyebut, lalu kalikan dengan pembilangnya masing-masing.
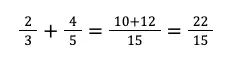
Pada penyelesaian di atas dari mana diperoleh nilai 10 dan 12?
15 dibagi 3 lalu hasilnya dikali 2, sehingga diperoleh nilai 10. Lakukan langkah yang sama untuk pecahan lainnya.
2. Pengurangan pecahan
Pada prinsipnya, pengurangan pecahan sama dengan penjumlahan.
Secara umum, pengurangan dibagi menjadi dua yaitu pengurangan bilangan berpenyebut sama dan berpenyebut berbeda.
a. Pengurangan pecahan berpenyebut sama
Pengurangan ini cukup mudah karena kamu hanya perlu mengurangkan pembilangnya saja. Berikut ini contohnya.

b. Pengurangan pecahan berpenyebut berbeda
Untuk mengurangkan bilangan yang penyebutnya berbeda, langkahnya sama persis dengan penjumlahan, yaitu dengan mencari KPK antara dua atau lebih penyebut. Berikut ini contohnya.
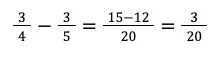
3. Perkalian pecahan
Perkalian pecahan termasuk operasi bilangan paling mudah jika dibandingkan dua operasi sebelumnya, yaitu cukup mengalikan pembilang dengan pembilang serta penyebut dengan penyebut. Berikut ini contohnya.
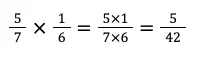
4. Pembagian pecahan
Langkah pembagian pecahan tidak sama dengan perkalian. Jika pada perkalian kamu bisa langsung mengalikan pembilang dengan pembilang serta penyebut dengan penyebut.
Pada pembagian, pertama kamu harus mengubahnya menjadi perkalian terlebih dahulu dengan syarat pembilang dibalik menjadi penyebut dan sebaliknya. Berikut ini contohnya.
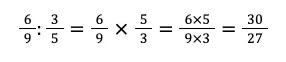
Sifat-Sifat Operasi Bilangan Pecahan Dan Contohnya
A. Sifat Penjumlahan Pecahan
1. Komutatif
Sifat komutatif adalah sifat pertukaran. Sifat komutatif penjumlahan pada bilangan pecahan dituliskan sebagai berikut:
| a/b + c/d = c/d + a/b |
Contoh:
1/2 + 1/3 = 1/3 + 1/2
1/4 + 1/5 = 1/5 + 1/4
2. Asosiatif
Sifat asosiatif adalah sifat pengelompokan. Sifat asosiatif penjumlahan pada bilangan pecahan dituliskan sebagai berikut:
| (a/b + c/d) + e/f = a/b + (c/d + e/f) |
Contoh:
(1/2 + 1/3) + 1/4 = 1/2 + (1/3 + 1/4)
(1/5 + 1/6) + 1/7 = 1/5 + (1/6 + 1/7)
3. Unsur Identitas
Unsur identitas penjumlahan pada bilangan pecahan adalah bilangan 0 (nol). Artinya, semua bilangan pecahan apabila dijumlahkan dengan 0 (nol), maka hasilnya adalah bilangan pecahan itu sendiri. Sifat identitas penjumlahan bilangan pecahan dituliskan sebagai berikut:
| a/b + 0 = 0 + a/b = a/b |
Contoh:
1/2 + 0 = 0 + 1/2 = 1/2
3/4 + 0 = 0 + 3/4 = 3/4
4. Invers
Invers suatu bilangan pecahan artinya lawan dari bilangan pecahan itu sendiri. Suatu bilangan pecahan dikatakan memiliki invers jumlah, jika hasil penjumlahan bilangan pecahan tersebut dengan inversnya (lawannya) hasilnya 0 (nol).
Invers dari bilangan pecahan a/b adalah bilangan pecahan -a/b, sedangkan invers dari bilangan pecahan -a/b adalah bilangan pecahan a/b. Hal ini dapat dituliskan bahwa untuk semua bilangan pecahan a/b, selalu berlaku:
| a/b + (-a/b) = (-a/b) + a/b = 0 |
Contoh:
1/2 + (-1/2) = (-1/2) + 1/2 = 0
3/4 + (-3/4) = (-3/4) + 3/4 = 0
B. Sifat Pengurangan Pecahan
Pengurangan merupakan lawan dari penjumlahan, sehingga berlaku sifat berikut:
| a/c – b/c = a/c + (-b/c) |
Contoh:
3/4 – 1/4 = 3/4 + (-1/4)
4/5 – 2/5 = 4/5 + (-2/5)
C. Sifat Perkalian Pecahan
1. Komutatif
Sifat komutatif adalah sifat pertukaran. Sifat komutatif perkalian pada bilangan pecahan dituliskan sebagai berikut:
| a/b x c/d = c/d x a/b |
Contoh:
1/2 x 1/3 = 1/3 x 1/2
1/4 x 1/5 = 1/5 x 1/4
2. Asosiatif
Sifat asosiatif adalah sifat pengelompokan. Sifat asosiatif perkalian pada bilangan pecahan dituliskan sebagai berikut:
| (a/b x c/d) x e/f = a/b x (c/d x e/f) |
Contoh:
(1/2 x 1/3) x 1/4 = 1/2 x (1/3 x 1/4)
(1/5 x 1/6) x 1/7 = 1/5 x (1/6 x 1/7)
3. Distributif
Sifat distributif adalah sifat penyebaran. Sifat distributif pada bilangan pecahan terdiri dari:
a. Distributif Perkalian Terhadap Penjumlahan
Sifat distributif perkalian terhadap penjumlahan pada bilangan pecahan dituliskan sebagai berikut:
| a/b x (c/d + e/f) = (a/b x c/d) + (a/b x e/f) |
Contoh:
1/2 x (2/3 + 4/5) = (1/2 x 2/3) + (1/2 x 4/5)
1/6 x (1/7 + 1/8) = (1/6 x 1/7) + (1/6 x 1/8)
b. Distributif Perkalian Terhadap Pengurangan
Sifat distributif perkalian terhadap pengurangan pada bilangan pecahan dituliskan sebagai berikut:
| a/b x (c/d – e/f) = (a/b x c/d) – (a/b x e/f) |
Contoh:
1/2 x (2/3 – 4/5) = (1/2 x 2/3) – (1/2 x 4/5)
1/6 x (1/7 – 1/8) = (1/6 x 1/7) – (1/6 x 1/8)
4. Unsur Identitas Perkalian Pecahan
Unsur identitas perkalian pada bilangan pecahan adalah bilangan 1 (satu). Artinya, semua bilangan pecahan apabila dikalikan dengan 1 (satu), maka hasilnya adalah bilangan pecahan itu sendiri. Sifat identitas perkalian bilangan pecahan dituliskan sebagai berikut:
| a/b x 1 = 1 x a/b = a/b |
Contoh:
2/3 x 1 = 1 x 2/3 = 2/3
4/5 x 1 = 1 x 4/5 = 4/5
D. Sifat Pembagian Pecahan
Pembagian merupakan kebalikan dari perkalian, sehingga berlaku:
| a/b : c/d = a/b x d/c |
Contoh:
1/2 : 3/4 = 1/2 x 4/3
1/5 : 6/7 = 1/5 x 7/6
Komentar
Posting Komentar